This is the second part in a 3-part series…
Part 2: Identifying and fixing errors in our game plan
Part 3: What to look for when analyzing video
Last time, we talked about how to use visualization to identify execution errors as they happen. Of course, doing so assumes that our visualized game plan is correct to begin with. But what if our visualized game plan itself is wrong? Before we can identify errors with our game plan, we need to consider how we go about coming up with our visualized game plan. While we’ve established that creating detailed visualizations is vitally important for going faster, how do we know what to even visualize??
Depending on our level of knowledge and experience, each of us has a different “program”; our own algorithm that we use to come up with our driving game plan. For example, someone brand new to driving probably has a plan built around simply staying on the track. Someone that has a bit of experience may have heard about setting up for a corner, so they build their game plan by trying to make big arcs through each corner. Someone more experienced might build their game plan by thinking about late apexing to get on the power sooner. You may take trail braking, induced rotation, surface conditions, and the capabilities of your particular car into account. Autocrossers may think about minimizing distance, etc.
Take a moment to pause here and really think about how YOU come up with your game plan; how you determine your line, how you determine what to prioritize, how you determine what to compromise. Upgrading our programming to come up with better game plans takes knowledge and experience and is built over time. In future posts, we will delve into using line theory (in painstaking detail) to craft a solid game plan ahead of time, but today, let’s focus on some of the (not so basic) basics to see how we can recognize errors in our game plan while we are on track.
Remember what our goal is
This may seem like something plainly obvious, but sometimes, in the pursuit of more complex answers we forget the simplest truths: Our goal as drivers is not to maximize speed, but to minimize time.
Let’s illustrate this with an example:
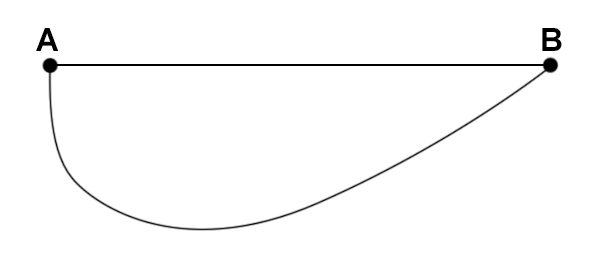
Imagine that we are in a car at rest at point A, and we have the goal of getting to point B, half a mile away, as quickly as possible. Hopefully it is obvious that the quickest way (i.e. the way that takes the least amount of time) is to accelerate in a straight line from A to B. However, we can take other paths that will get us to B at a higher speed. In this simple example, it is easy to see that by providing a longer distance over which to accelerate, even though the curved path will get us to B at a higher terminal speed, the straighter path takes less time. The point here isn’t about curved vs. straight paths, rather that we need to always be focused on reducing time, not maximizing speed. Time = distance/speed, so if we drive a much greater distance in order to achieve the higher speed, we will lose time.
Let’s take a look at another example:
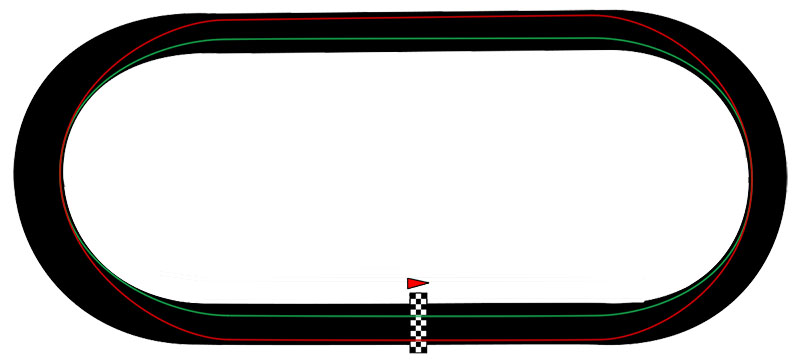
Imagine now that we are on an oval race track without any banking. With the amount of grip our car has, imagine that hugging the tightest possible line would require us to take the corners at 120 mph, but taking a classic racing line (with a larger corner radius) would allow us to take the corners at 160 mph. In such a scenario, what line would you take? While you may be tempted to say you would take the classic racing line, the correct answer is that we do not have enough information to answer the question! We need to know the speed and acceleration potential of the car. If we are driving a car that can achieve 200+ mph, then certainly, the classic racing line would be better than the tightest line. But if we are driving a car that can only achieve a maximum speed of 135 mph, driving the wider classic racing line (red line) would actually take more time because we would be driving extra distance, without being at a speed that necessitates that distance. In such a scenario, we would want to drive a line that is just wide enough to keep us on the limit of traction (green line) because we would avoid driving a greater distance at the same speed. Remember, time = distance/speed. So if we increase the distance without increasing speed, the amount of time taken will increase.
All of this may seem trivial in the context of such simple examples, but consider how easy it is to fall into the trap of applying common racing rules (set up for a corner, drive wide arcs, use a late apex, backside the cone, etc) when we think about how we may want to drive around a track, without analyzing whether those rules apply in each particular situation. We tend to treat each of those rules as gospel, and apply them blindly, failing to identify situations where we may be losing time. Instead, when we understand why those rules exist and when they apply (and don’t apply), we become armed with the information needed to identify errors in our game plan.
Let’s work through a scenario
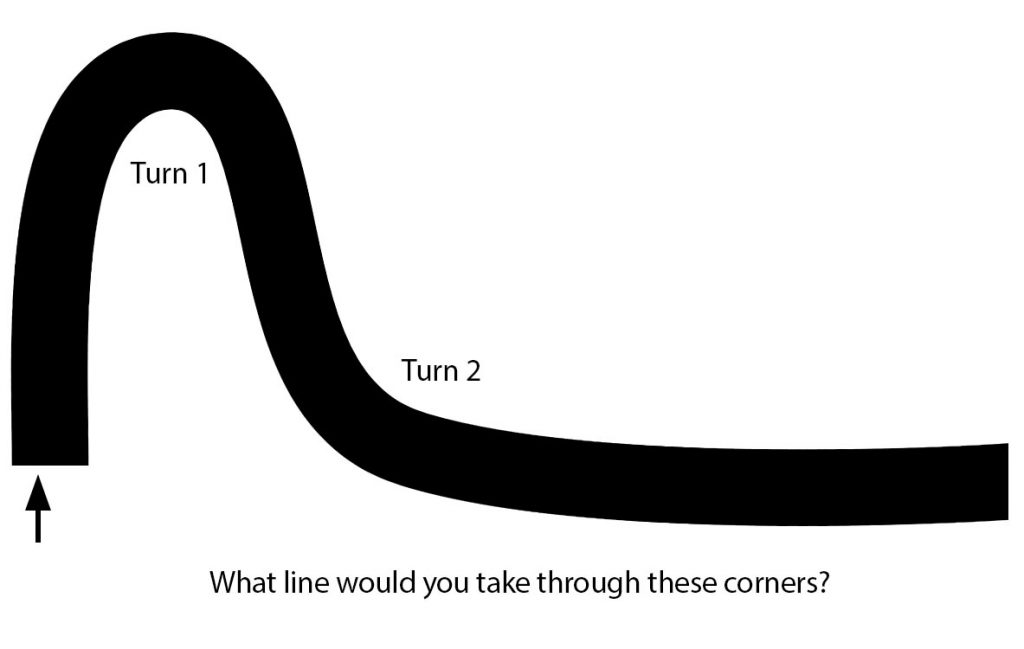
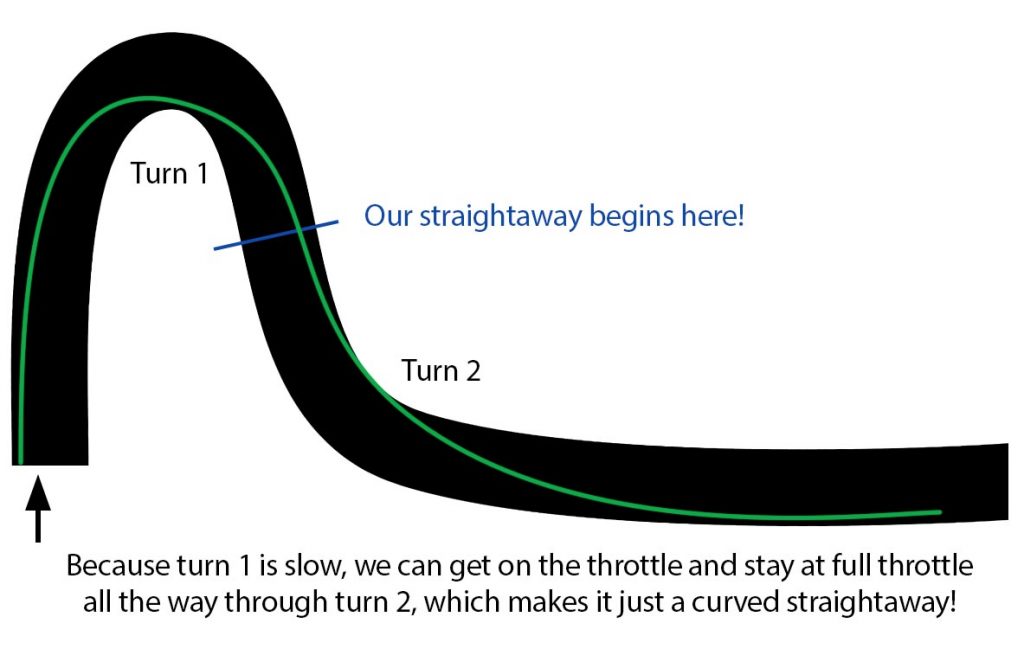
Consider a scenario as depicted here, where you approach a tight right hander, which is followed by a more open left hander, that leads onto a long straightaway. Before scrolling down and reading the analysis and explanation, just look at the illustration here and try to figure out what your game plan would be.
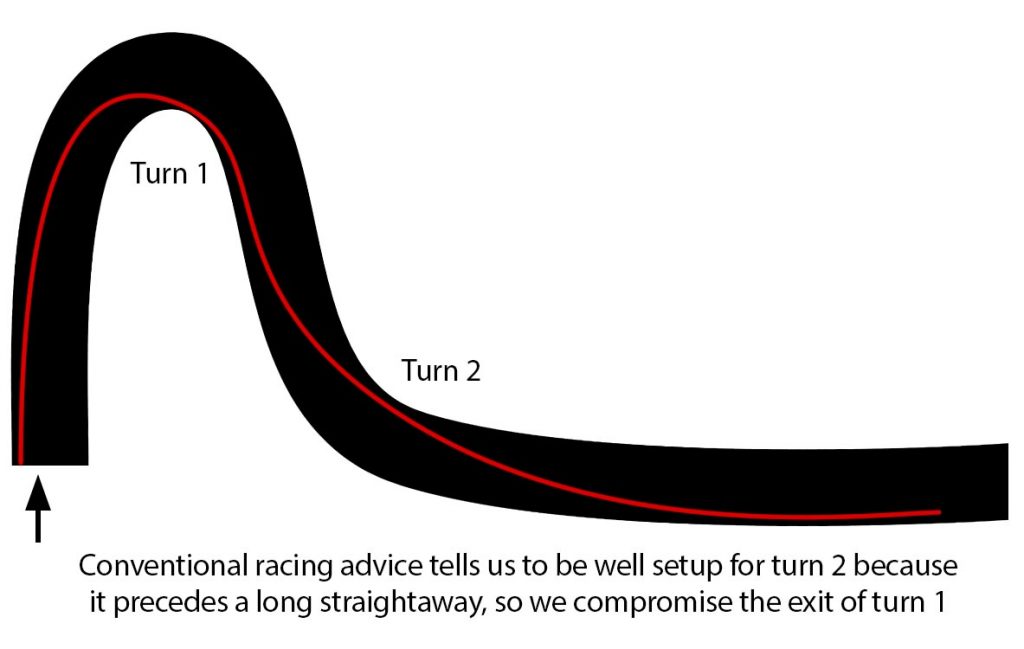
The usual advice from books, other drivers, etc. is that the most important corner is the one leading onto a long straightaway, and that it is of utmost importance to have the best line possible through that corner in order to maximize our speed on the subsequent straightaway. That is good advice in general, and thus, it would seem that the ideal approach to this sequence of corners would be to approach turn 1 with a wide entry, but to keep it tight on the exit (i.e. stay to the right side of the track) in order to maximize the radius for turn 2 so that we carry the greatest possible speed through onto the straightaway. In essence, we are willing to sacrifice the exit of turn 1 because of the payoff gained through turn 2.
However, just as with the oval example above, the correct answer to this problem is actually “it depends”. Our optimal line through the turns depends on (1) the speed we would be able to take each turn if we were considering each one independently, and (2) the acceleration potential of our car.
Imagine that taking an ideal line allows us to go around turn 1 at 35 mph. But in order to take a tight line (so we can be well set up for turn 2) we had to slow down to 30 mph. By doing so, we are able to straighten out turn 2, and are able to accelerate without interruption all the way through the corner. Most drivers would think they have done all they can to optimize this sequence of corners, but there is more time to be found. The key is in paying attention to whether we were at the limit of grip when entering turn 2. In this example, let’s assume that turn 2 allows us a maximum speed of 80 mph. Given that we slowed down to 30 mph for turn 1, chances are that unless we are in a very powerful car, we weren’t able to accelerate from 30 mph to 80 mph until we got all the way through corner 2. This means we were under the limit of grip for that entire corner!
What this tells us is that we could have carried more speed through turn 1, and been less well set up for turn 2 without hurting our ability to accelerate through the corner. By taking a more optimal line through turn 1 at 35 mph, even though we are not as well positioned for the entry of turn 2, we are still able to accelerate all the way through the corner because we are under the speed threshold for turn 2. This is the same concept as the oval example above, in that we do not need to set up wide for turn 2 because we are not traveling at a speed that requires the extra width/distance. Any time we drive extra distance while not traveling at a speed that requires the extra distance, we are losing time.
The key to being able to identify errors in your game plan while you are on track is being able to (on the fly) analyze the moments that you are under the limit of grip, and figuring out if there is anything you can do differently in and leading up to those moments.
Reframing what a straightaway is
It is important to realize that a straightaway is any part of the track where we are at full throttle; it does not matter if it is curved, or if it looks like a slalom. If we approach a curve, or a slalom, or any section at a speed such that it allows us to go through that section at full throttle, then for our purposes that part of the track is a straightaway. When we look at it this way, turn 2 in the example above isn’t a turn at all; it is just a curved straightaway, and we would want to use the full width of the track on the exit of turn 1 to get the best run onto the straightaway.
It should follow naturally that because different cars have different speed, acceleration, and grip capabilities, what turns into a straightaway for one car may not be a straightaway for another car. This tells us that the right line is not always going to be the same for all cars!
TAKE ACTION: During a lap, pay attention to every portion of the track where you are not at the limit of grip. Is there anything you can do to carry more speed out of preceding sections and into the section where you are under the limit? Is there anything you can do to cut distance when you are under the limit?
TAKE ACTION: We talked through one scenario where we need to be analytical and not apply the rules blindly; a tight corner followed by a more open corner. Think through other scenarios and see if you can figure out how the rules change for other combinations of corners. If you want a few concrete (no pun intended) examples to think through, consider the lines through turn 1-2, turns 7-8, and turns 13-14-15 at the Circuit of the Americas. Almost every autocross course has “hidden” straightaways as well, disguised as corners.
Let’s close this post with a thought exercise
We mentioned above that time = distance/speed, and that we should only increase distance if we can also increase our speed. With that in mind, imagine that we are now in a car on a perfectly circular race track with an inner radius of 200 feet, and an outer radius of 300 feet. What is the fastest way around this track? Driving the widest line will certainly yield the highest speed, but is the higher speed enough to offset the greater distance we are traveling on the outer circumference compared to driving a tighter line at a lower speed? What implications does this have for our line selection and game plan?



Assuming the car has negligible aero, I’m thinking that since the force your tires essentially have to act against is the car’s kenetic energy, the inside line would be the fastest. As the force your tires have to counter increases with the square of the speed of the vehicle, rather than linearly.
You are absolutely right. Said in other terms… the radius of a corner and the square of the velocity increase in proportion. As a result, the increase in velocity around a larger circle is not enough to counteract the greater distance. This has interesting implications for line selection even on non-circular race tracks 🙂
Indeed. Although I always find myself worrying about “scrubbing” speed when I hold the car to a tighter exit vs using the whole track even if not necessitated by traction limitations.
Would that then introduce another compromise situation where you balance this conversations topic against your cars horse power? Looking at it from a standpoint of the car’s diminishing acceleration ability with increasing speed. And allow that trade-off to fine tune the extent of your corner exit?
We are starting to touch on topics that would take multiple posts to cover in sufficient details, and cannot be explained in comments 🙂
In short, being tight around a circle does not necessarily mean being tight on exit. Keep in mind that when driving around a circle, there is NO exit. And absolutely, the acceleration capability we have (whether because of the car’s power, or the diminishing acceleration ability at higher speeds) most certainly influences the shape of the curve we would take around a corner.
A Miata should take the smaller radius, while a Z 06 should take the outside Lane….score 100?
Not quite Dave. Ignoring cars that have lots of aerodynamic aids, all cars should take the tightest line. The reason is explained in the comment above.
there still may be some subtle differences between say an MR2 and a Z06 in the road course example above though. Which was outlined well in the article 🙂
There absolutely WILL be differences between the line taken on a road course between an MR2 and Z06 🙂
For the circle – is it 1 lap or endless? Is there a way to hot lap in/out? If so, does hot lapping lend to starting on the wider/higher velocity line to take advantage of increased levels of grip/speed via trail braking up to a certain point in the arc?
No way to hot lap in/out. All driving is on the circular track only.
p.s. The answer is that hugging the inside will be the fastest way.